Summary:
State estimation is a core function of any battery management system (BMS) in order to ensure safe operating conditions and to prolong the lifetime of the energy storage system. In this context the state of charge (SOC) is an important indicator for the remaining useable battery capacity. This variable is not a measurable value, but rather a state that has to be estimated from battery data. This state estimation is commonly executed by a filter algorithm called extended Kalman filter (EKF). [1]
The Kalman filter estimates the state vector x_{k+1} as a function of the measured input and the state vector at time step k. The output vector y_k is computed in a similar manner. Noise terms are added characterizing the uncertainties of measurement and of the equivalent circuit model. This results in two model equations for the EKF.
The noise parameters are modelled as zero-mean white Gaussian stochastic processes. Their covariance matrices play a crucial role regarding the estimation accuracy and the convergence behavior [1].
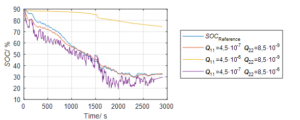
In many articles about state estimation with Kalman filtering the covariance matrices are not specified and therefore the results are not reproducible [2]. However, the articles, which provide information about these parameters, show values within the range of 10^{-12} [2] to 10^2 [3]. The preview picture shows the influence that slight changes of the diagonal elements of the covariance matrix have on the estimation accuracy.
Presently, the correlation between the matrix entries and the filter behavior is not known and the programmers of the Kalman filters have to rely on their experience in finding the optimal covariance parameters for their respective filter-model configuration [2].
For this reason, a parameter study is conducted in order to provide a deeper understanding of the influence of the covariance matrices for the model as well as for the measurement uncertainties.
Similar to Campestrini’s [2] rules of thumb, the study shows that small values for the covariance of the model error lead to small corrections by the filter, because it relies more on the model than on the measured data. Therefore, the tuning parameter for the state entry of the SOC should be initialized with a value close to zero while the parameters for the RC-voltages should be chosen in a range two to four magnitudes higher.
In conclusion, this study provides a better understanding of the interaction between model and filter parameters and their influence on the estimation results.
References
[1] Plett, G.L.: Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs. In: Journal of Power Sources 134 (2004), Nr. 2, S. 252–261
[2] Campestrini, C. ; Heil, T. ; Kosch, S. ; Jossen, A.: A comparative study and review of different Kalman filters by applying an enhanced validation method. In: Journal of Energy Storage 8 (2016), S. 142–159
[3] Xu, J. ; Mi, C.C. ; Cao, B. ; Cao, J.: A new method to estimate the state of charge of lithium-ion batteries based on the battery impedance model. In: Journal of Power Sources 233 (2013), S. 277–284
We are happy to forward your request / feedback.