Introduction of a variable discretization of a transmission line model for graphite electrodes

Summary:

Fast charging applications require high currents which can lead to an accelerated ageing of the battery. One reason is the capacity loss evoked by unwanted lithium plating on the anode during charging, especially at low temperatures and elevated states of charge (SOC). To avoid this, a precise prediction of the anode potential is required.
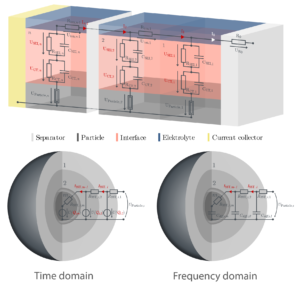
Most state-of-the-art battery models do not provide spatial information on the state variables and are therefore not as accurate as physical-chemical models. However, these models are real time capable and much easier to parametrize. Transmission line models (TLM) enable spatial resolution thus keeping the simplicity and comfortable parameterization of state-of-the-art models. The model consists of a discretized electrical model of which each string contains a model for ionic transport, charge-transfer (CT), solid-electrolyte-interphase (SEI) and solid-state-transport. The latter is simulated with another TLM representing the SST in an ideally spherical particle. The parameters of the distributed elements are calculated with the relative element / particle size and the according global parameter. The model therefore consists of seven model parameters equaling the number of an equivalent circuit with an ohmic resistance and three RC elements. The seven TLM parameters are independent of the number of elements and particle shells, whereas the achievable precision behaves contrary to the computational effort. Though more elements produce more precise results, they also increase the simulation time and required memory, which is a problem on battery management systems (BMS).
To overcome this issue, we introduce a variable discretization for the electrode and the particle with small elements near the separator and on the surface of the particles. Without changing the number of elements and particles, we can increase spatial resolution at the separator and the particles surface, where the most dynamic changes occur during load. The effects of larger elements at the current collector and the inner particles are neglectable due to the reduced dynamic changes there. Alternatively, the number of necessary elements can be reduced while maintaining the same level of spatial resolution at the crucial regions. The variable discretization only requires minor additional calculations in the pre-processing. All in all, this leads to a reduced computational effort and memory requirement. For the realization of variable element sizes, we use mathematical function approaches. Besides the most common types of functions, we also introduce an arctangent function offering an s shaped increase in element size. The courses of the functions are customizable by adjusting the coefficients in given limits to fit user defined demands while maintaining essential requirements like positive element sizes and monotonic increase in size.
With the presented method we can combine the benefits of fast computation and high precision, making electrochemical models with spatial resolution accessible for an application in a BMS.