FEM based modelling of lamellar LiFePO4 electrodes

Summary:

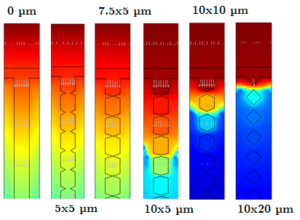
Porous electrodes in lithium-ion batteries increase the active area and thus can be used to achieve higher power densities and more uniform current distributions. The freeze-casting (ice- templating) method enables the fabrication of high porous lamellar structured lithium-iron(III)- phosphate cathodes. The variation of temperature and supersaturation leads to different morphologies in pore shapes by ice-templating (e.g. cellular, lamellar, dendritic or honeycomb) [1]. In comparison to cellular pores, the lamellar morphology provides a higher specific capacity and a lower loss of energy density [2]. In this work, a two-dimensional physicochemical model of lamellar cathode structures is developed in COMSOL Multiphysics. This model is used to study the influence of width and distance of the lamellas as well as short circuits between lamellas due to dendrites. The experimental data and some assumptions about the lamella sizes and orientations are the fundamentals of the geometric model. The variation of geometrical and material parameters affects the ion transport in the electrolyte and porous cathode, the electric conductivity and the intercalation of lithium into the cathode. Hence, changes in the battery voltage and the lithiation of the lamellas are investigated. The model shows that the influence of the lamella width on the cell voltage is negligible. The ratio between lamella width and distance as well as the dendrites between the lamellas are the main influencing factors on the cell performance. Structured electrodes with free electrolyte channels can improve the performance and capacity of lithium-iron-phosphate batteries due to a uniform lithiation of the lamellas and an increase of the active surface. Nevertheless, a blockage of an electrolyte channel by dendrite growing leads to a massive overpotential within the electrolyte which ends in a very fast capacity loss. This loss depends on the height and thickness of dendrites. Also, the high current capability suffers from the channel blockage, as solid diffusion becomes the dominant mass transport.

References:
[1] S. Deville, Journal of Materials Research 28 (2013) 2202–2219.
[2] S. Zavareh, A. Hilger, K. Hirselandt, O. Goerke, I. Manke, J. Banhart, A. Gurlo, Journal of the Ceramic Society of Japan 124 (2016) 1067–1071.